Visualize and calculate how much your money can grow with the power of compound interest
Take your wealth planning to the next level with my Wealth Planning Toolkit for Google Sheets – just $20.
Plan for recurring monthly income over different time periods as well as windfalls and one-time purchases in the future.
Includes 10 year Net Worth Tracker with Dashboard, Asset Rebalancing Calculator, and advanced FIRE and Coast FIRE Calculators.
The power of compound interest
Albert Einstein once famously said:
“Compound interest is the 8th wonder of the world. He who understands it, earns it; he who doesn’t, pays it.”
Einstein couldn’t have put it better. Compound interest truly is one of the most powerful forces in the universe, and it can both work for you in the case of growing investments or against you in the case of compounding debt. The key ingredient for compounding growth is time. You can adjust the inputs in the above calculator to see how when given enough time, even a small initial investment can grow to a significant sum of money.
Using this calculator
This interactive calculator makes it easy to calculate and visualize the growth of your investment thanks to compounding interest.
- Initial investment is the starting value of your investment, also known as the principal.
- Length of time in years is the length of time over which your investment will grow.
- Monthly contribution is a recurring amount that you contribute to your account each month.
- Interest rate is the annual interest rate of return of your investment. For reference, the S&P 500 has returned about 7% annually adjusted for inflation since it was started in 1926.
- End investment value is the final value of your investment at the end of your investing period.
How does compound interest work?
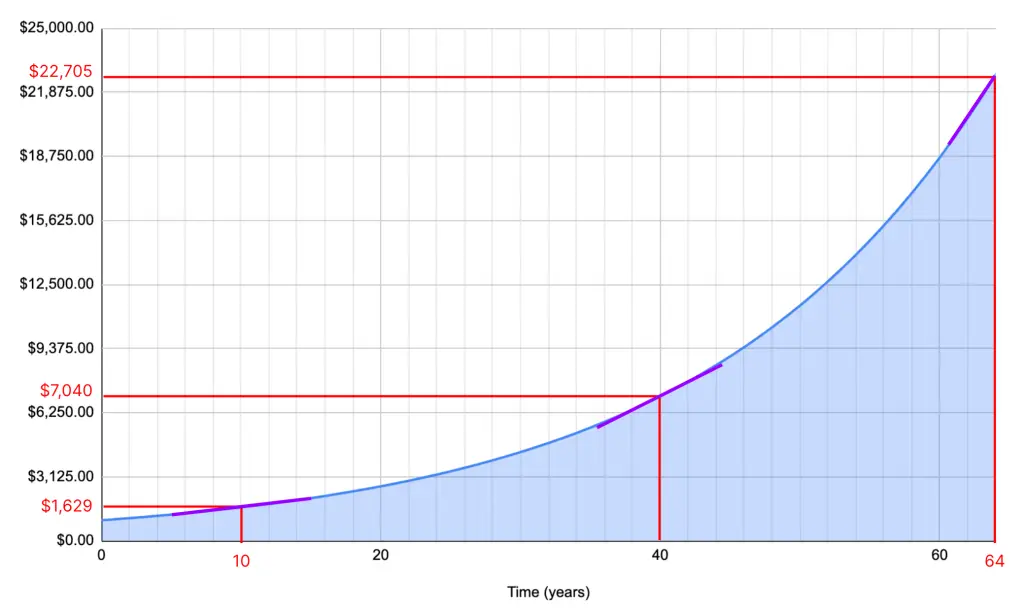
Compound interest is essentially a snowball effect of interest that is accrued on an initial investment of money. To understand how it works, let’s start with an example. Say you begin with $1,000 and put it into an investment that returns 5% annually. The chart below shows the growth of your investment over the first 10 years.
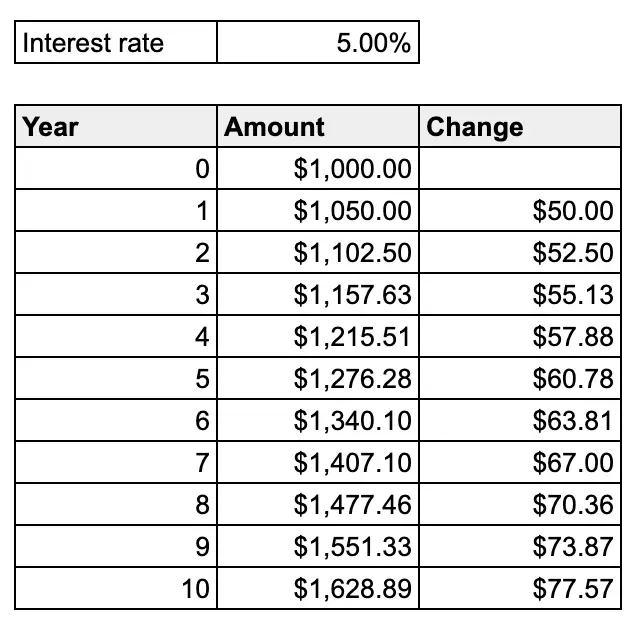
If you look at the change column, you can see that the total account increases by a greater amount each year. This is the nonlinear part of exponential growth, where the rate-of-change is increasing. This becomes especially powerful over longer periods of time. The element of time is crucially important to wielding the power of compounding growth.
While the savings account only grew about $78 year-over-year after the 10th year, or 8% of the initial amount, by the 40th year, the savings account will grow $388 year-over-year or about 39% of the initial amount. By year 64, the account will grow by $1,030 year-over-year, more than the initial $1000 that was put in to start the account! In the first few years, the compounding starts slowly and is hard to notice, but over time it becomes immensely powerful.